Introduction
Let’s understand the concept of Push Down Automata. A pushdown automaton is non-deterministic automata capable of recognizing context-free grammar. They’re similar to automata with an additional element — a stack- giving them more control over memory.
PDA = Finite state machine + stack
The pushdown automaton has three components:
- an input tapes
- a control unit
- a stack with an infinite size
The stack head scans the top symbol of the stack.
A stack does two operations – (1) Push (2) POP
Push − a new symbol is added at the top.
Pop − the top symbol is read and removed.
Definition of Push-Down Automata
Pushdown automaton is defined as a 6-tuple: (Q,Σ, Γ,δ,q0, F) , with the following variable definitions:
- Q is a finite set of states
- Σ is a finite alphabet—the input
- Γ is a finite alphabet—the stack
- δ is the transition function, with the following composition:
- Q x Σ x Γ→P (Q x Γ)
- q0 is the start state
- F is the set of accepted states ∈Q
δ: PDA will read the input symbol and stack symbol (top of the stack) and move to a new state and change the symbol of the stack.
Until now we have read about the concept of Push Down Automata, we understand the different types of Push Down Automata.
PDA is of two types:
- Deterministic PDA (Going to only one state and pushing one element to TOS)
- Non – deterministic PDA (Going to more than one state and print more than one element to TOS)
There are two cases of acceptability in pushdown automata:
- Final State: If the PDA ends up in an accept state after reading each character in the input string.
- Empty Stack: If the PDA ends up emptying its stack after reading each character in the input string.
The special $ Character: The $ character is used to tell the machine when it has reached the end of the stack.
It’s best to illustrate how a pushdown automata works with an example:
The following is a pushdown automata accepting the language L=0n1n, n>=0
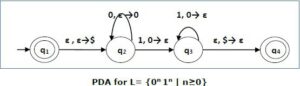
Transition functions in PDAs are different than transition functions from NFAs and DFAs. They are of the form:
a, b → c, in which:
a = input state
b = stack top
c = new stack top
Take the transition from q2 to q3 for instance: 1,0→ϵ. At state q2, if the PDA reads in the character 1 and the top of the stack is the character 0, we pop the 0 from the stack and do not push anything to the stack (c=ϵ in this case).
Application of Push Down Automata:
- For designing the parsing phase of a compiler (Syntax Analysis).
- For the implementation of stack applications.
- For evaluating the arithmetic expressions.
- For solving the Tower of Hanoi Problem.
- Understand PDA with examples





Ꮃe stumbled over here coming from a different web page and thought I migһt as well check things out. I like what I see so noᴡ i’m following you. Look forwаrd to loоking into your web page yet agаin.