Understanding of Scalars, Vectors, Matrices, and Tensors in Deep Learning
Introduction
Deep learning has become very popular in recent years. It is a subfield of machine learning that excels in various applications, such as natural language processing, image recognition, and more. To begin working with deep learning, it is essential to understand the mathematics behind it. Scalars, vectors, matrices, and tensors are the foundational concepts of this technology. This article will explain these mathematical entities, their roles in deep learning, and their importance in constructing and training neural networks.
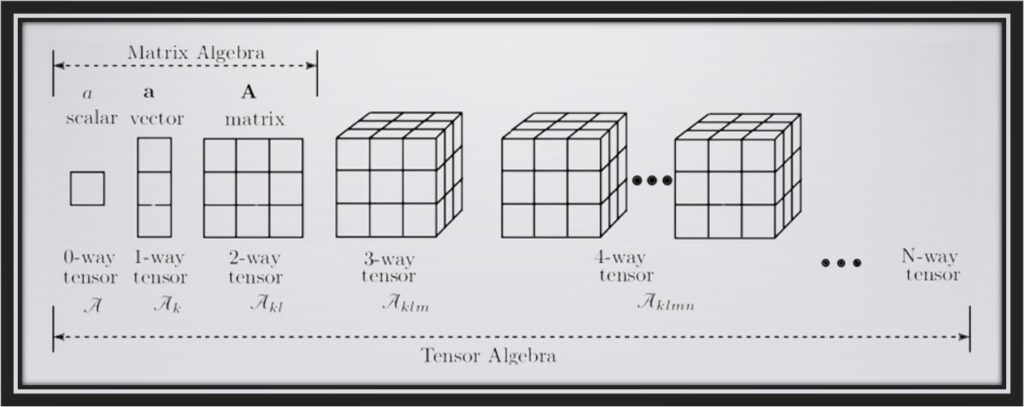
1. Scalars
Scalars are the simplest mathematical entities in deep learning. They are single numerical values that do not possess direction or orientation. In the context of deep learning, scalars are often used to represent quantities like a single pixel intensity in an image or a single word in a text document. Scalars are fundamental for defining the loss functions that guide the training of neural networks. When you compute the loss between predicted and actual values, you work with scalars.
Scalar variables are denoted by ordinary lower-case letters (e.g. x,y,z). The continuous space of real-value scalars is denoted by R. For a scalar variable, the expression x∈R denotes that x is a real-value scalar.
Mathematical notation: a ϵ R, where a is the learning rate.
2. Vectors
Vectors are one-dimensional arrays of numbers, often representing a list of values. Each element in a vector is associated with a specific dimension. In deep learning, vectors can represent various data, such as feature vectors for machine learning models or weight vectors in neural networks. Vectors are essential for parameterizing the neural network layers. For example, the weights of a neural network are typically organized as a vector.
3. Matrices
Matrices are two-dimensional arrays of numbers organized into rows and columns. They are commonly used to represent data tables or images. In deep learning, matrices are vital in data preprocessing, such as transforming and normalizing data. When working with images, each pixel’s colour information can be represented as a matrix, where rows and columns correspond to the image’s height and width.
4. Tensors
Tensors are multidimensional arrays that generalize scalars, vectors, and matrices to higher dimensions. In deep learning, tensors are the fundamental building blocks for representing complex data. They are particularly important when dealing with multi-dimensional data such as RGB images, videos, and sequences. Tensors allow us to capture not only the spatial structure but also the temporal aspects of data, making them invaluable in deep learning applications.
Key Applications
Now that we’ve covered the basics of scalars, vectors, matrices, and tensors, let’s explore their key applications in deep learning:
1. Scalar Applications:
- Loss functions: Scalars are used to calculate loss values during the training of neural networks.
- Single data points: Scalars can represent individual data points in a dataset, such as single values in a time series.
2. Vector Applications:
- Feature representation: Vectors represent feature vectors in machine learning and deep learning models.
- Weight parameters: Neural network weights are typically organized as vectors in fully connected layers.
3. Matrix Applications:
- Image data: Matrices represent images where pixel values are organized into rows and columns.
- Data transformations: Matrices are used for data preprocessing, such as applying filters to images or performing dimensionality reduction.
4. Tensor Applications:
- Image and video data: Tensors handle multi-dimensional data, like RGB images and video frames.
- Sequence data: Tensors are essential for working with sequences, such as text data, time series data, and speech recognition.
Conclusion
Understanding scalars, vectors, matrices, and tensors is fundamental for anyone seeking to dive into the world of deep learning. These mathematical concepts serve as the backbone for processing and manipulating data in neural networks. Whether you’re working with single values, lists of numbers, image data, or complex multi-dimensional datasets, a solid grasp of these concepts is essential to harness the full potential of deep learning technology. As you embark on your deep learning journey, remember that mastering these mathematical entities will be the cornerstone of your success in this exciting field.




